分类问题是机器学习中的一种常见问题。
在机器学习领域，有很多分类算法。而神经网络的优势在于：几乎可以实现任意复杂的分类边界，无误差地实现训练集上的分类^3。

由于神经网络的拟合能力很强大，常常容易产生过拟合，所以需要进行相应的处理。
而且，神经网络的可解释性往往是个非常大的难题。

线性回归的机器学习解释

线性回归是一个有着两百年历史从一些输入输出对组中推断出一般函数的技巧。
线性回归所做的基本上就是监督式机器学习：给定训练样本，「学习」一个函数，每一个样本数据就是需要学习的函数的输入输出数据。并且这个函数能够很好的泛化到不在训练集中的输入值上。并且可以通过测试数据来检验泛化的效果^4。

分类问题和逻辑回归

逻辑回归，就是把线性回归的思路应用到分类问题上^2：

空间中有两群点，一群是圆点“〇”，一群是叉点“X”。我们希望从空间中选出一个分离边界，将这两群点分开。

{% asset_img logistic01.png 逻辑回归原理 %}

具体过程如下图：

{% asset_img logistic02.jpg 逻辑回归过程 %}

一个心理学家弗兰克· 罗森布拉特(Frank Rosenblatt)构想了感知机，使用简化的数学模型解释大脑神经元如何工作：

{% asset_img perceptron.jpg 感知机 %}

取一组二进制输入值$x_i$（附近的神经元），将每个输入值乘以一个连续值权重$w_i$（每个附近神经元的突触强度），并设立一个阈值，如果这些加权输入值的和超过这个阈值，就输出1，否则输出0（同理于神经元是否放电）。

对于感知机，绝大多数输入值不是一些数据，就是别的感知机的输出值。但有一个额外的细节：感知机有一个特殊的偏置输入，$x_0=1$。这样可以通过调节其权重$w_0$，使得感知机能够适应更广泛的输入值。

赫布认为知识和学习发生在大脑主要是通过神经元间突触的形成与变化，即赫布法则：

当细胞A的轴突足以接近以激发细胞B，并反复持续地对细胞B放电，一些生长过程或代谢变化将发生在某一个或这两个细胞内，以致A作为对B放电的细胞中的一个，效率增加。

如果感知机的 偏置 输入不是固定为1，而是一个偏置 函数：

从感知机有随机的权重和一个训练集开始
对于训练集中一个实例的输入值，计算感知机的输出值
如若感知机的输出值和实例中默认正确的输出值不同：
- 若输出值应该为0但实际为1，减少输入值是1的例子的权重
- 若输出值应该为1但实际为0，增加输入值是1的例子的权重
对于训练集中下一个例子做同样的事，重复步骤2-4直到感知机不再出错

则感知机就有了记忆和学习的功能。

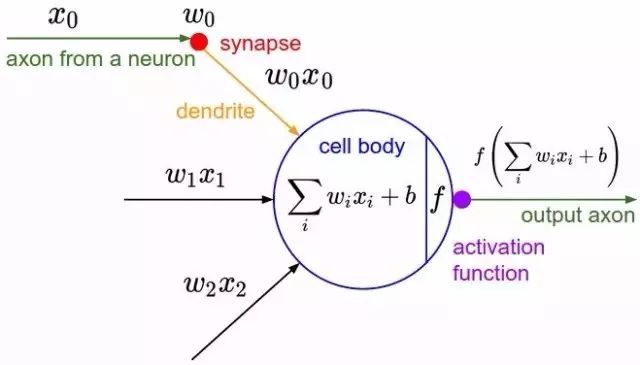
从数学角度来看，感知机的函数为：

$$f = \sum_{i=0}^{n}w_ix_i+b$$

其本质是一种线性变换。

单个感知机智能处理二元的逻辑分类。如果由多个感知机组合，就可以处理多分类问题：

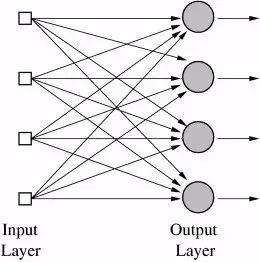
如上图，将多个感知机连接起来，使得所有的感知机输入都相同，但调节后每次只有一个感知机输出，
就形成了一个多元的分类器。这种结构称为人工神经网络（ANN，Artificial Neural Networks）。
在ANN中，感知机被重新命名为“神经元”。

我们可以看出，这个神经网络只有一层，即“输出层”。

尽管将感知机组成了单层的网络，但其本质上仍然是线性变换，处理能力很有限。
比如，感知机不能学习简单的异或(XOR)——因为XOR不是线性可分的。

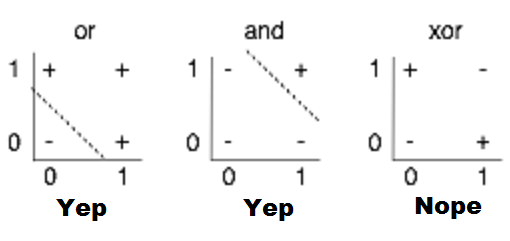
这种网络的处理能力，与逻辑回归完全相同。

但是神经网络有一个好处，就是很容易增加层数(即神经网络的深度)。

比如，一个三层(单隐层)的神经网络，对n个逻辑回归的n个输出再做m个逻辑回归:

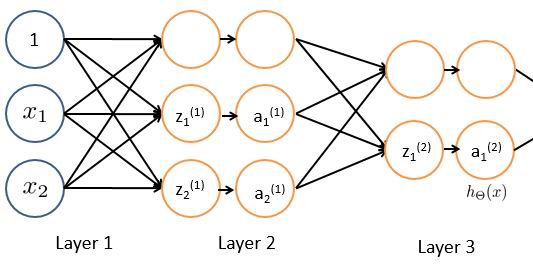
而且这个过程可以无限递归下去：

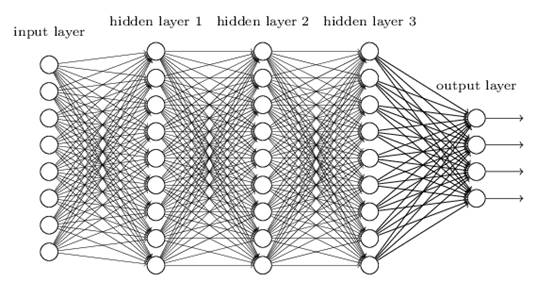
在多层神经网络中，通常把层分为输入层、隐藏层、输出层；所谓的深度学习，就是对有较多隐藏层的神经网络进行训练。

多层神经网络的数学解释是：

通过连续多次简单的逻辑回归，最终使得复杂问题线性可分。

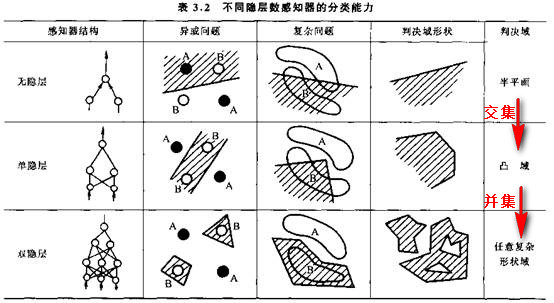
数学家们经过严格的数学证明，双隐层神经网络能够解决任意复杂的分类问题。
尽管如此，多个隐藏层可以逐步提取特征，使得后续层不必处理嘈杂庞大的原始数据，
能够简化问题和提高效率。因此深度学习还是很有必要的。

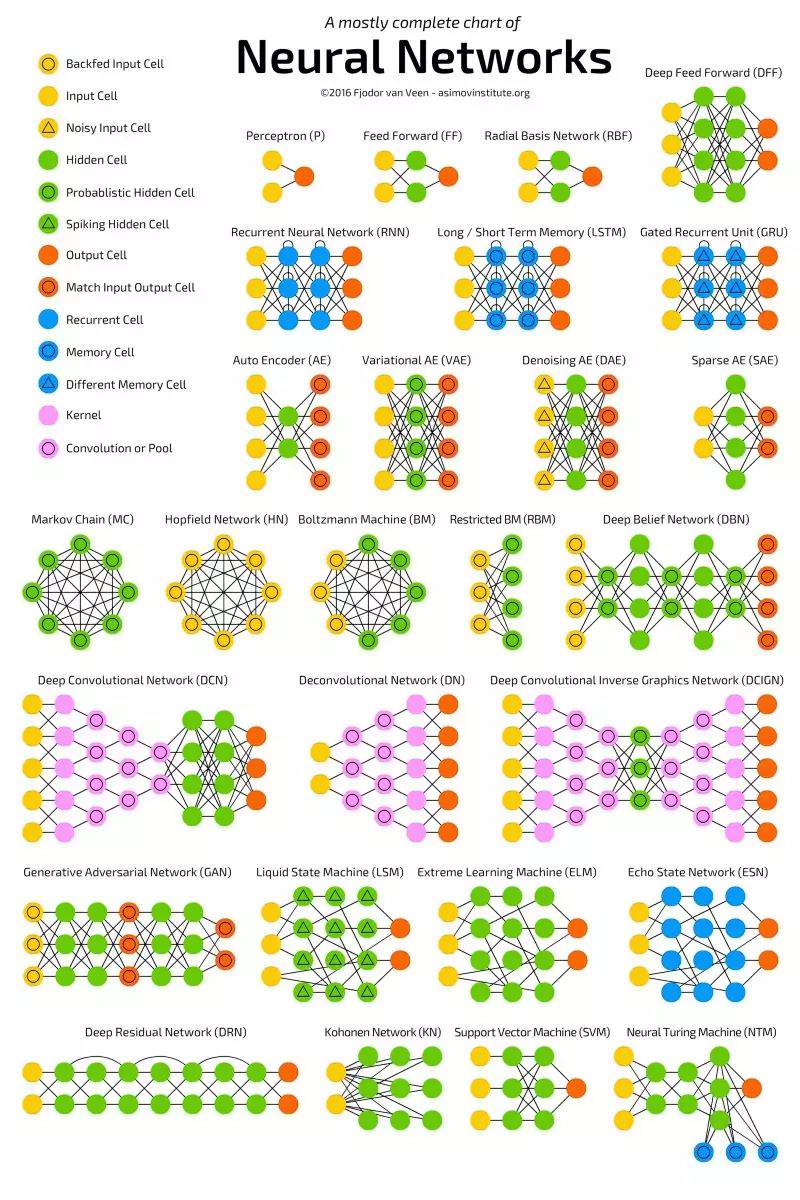
经过多年的发展，已经形成了很多种变体。下图展示了最流行的神经网络变体，可参考这篇博客 (http://www.asimovinstitute.org/neural-network-zoo/)。