心内求法

Holbrook的个人博客

0%

逻辑回归

Posted on Edited on In

逻辑回归(logistic regression)，虽然本质上属于广义线性回归，
但是因变量Y是离散值，一般用来解决分类问题。

与其他分类方法相比，逻辑回归对于每一个输出的对象都有一个对应类别的概率。

逻辑回归算法本质上是回归，即是通过一系列特征数据回归出某种情况出现的概率。
在此基础上再引入了逻辑函数，就可以用来分类。

逻辑回归的推导

逻辑回归(logistic regression)，虽然本质上属于广义线性回归，
但是因变量Y是离散值，一般用来解决分类问题。

与其他分类方法相比，逻辑回归对于每一个输出的对象都有一个对应类别的概率。

逻辑回归算法本质上是回归，即是通过一系列特征数据回归出某种情况出现的概率。
在此基础上再引入了逻辑函数，就可以用来分类。

对于多元线性回归，有：

$$f(X)=b_0+b_1x_1+…+b_nx_n$$

如果希望结果是一个逻辑值(True-False)，就需要引入逻辑函数进行变换。

这里引入sigmoid函数作为逻辑函数。sigmoid函数的形式为：

$$f(x)=\frac{1}{1+e^{-x}}$$

该函数的图像如下：

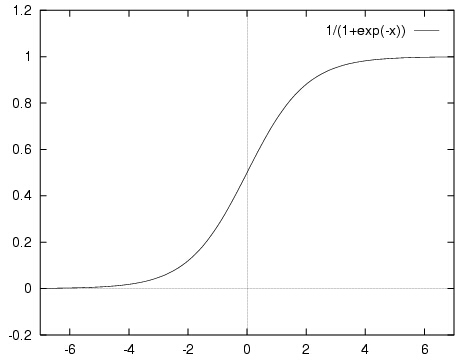
其优点在于：

  • 定义域在全体实数，值域在[0, 1]
  • 在0点值为0.5
  • 容易求导

缺点是饱和的时候梯度太小。

对于逻辑函数，可以认为 f(x)>0.5 和 f(x)< 0.5 是两种结果类型。

对于0-1问题，如果：

  • 结果为1的概率为p。 P(y=1)=p
  • 结果为0的概率为1-p。P(y=0) = 1-p

则期望值 $E(y)=1p + 0(1-p) =p$

再引入 logit 变换, 使得概率p 与自变量之间满足线性关系，则有 $logit(p)=ln \frac{p}{1-p}=b_0+b_1x_1+…+b_nx_n$

经过推导可以得出： $p=\frac{1}{1+e^{-(b_0+b_1x_1+…+b_nx_n)}}$ , 满足sigmoid函数的形式。

接下来只需要用线性回归的方法，拟合出该式中n个参数即可。

用 scikit-learn的逻辑回归模型分析鸢尾花数据集

import pandas as pd
import warnings 
# 用来忽略seaborn绘图库产生的warnings
warnings.filterwarnings("ignore")
import seaborn as sns
import matplotlib.pyplot as plt
sns.set(style="white", color_codes=True)
%pylab inline

Populating the interactive namespace from numpy and matplotlib

from sklearn.datasets import load_iris
iris = load_iris()
df = pd.DataFrame(iris.data,columns=['sepal_length','sepal_width','petal_length','petal_width'])
df['target']=pd.Series(iris.target)
df.head()
Out[3]:
sepal_length sepal_width petal_length petal_width target
0 5.1 3.5 1.4 0.2 0
1 4.9 3.0 1.4 0.2 0
2 4.7 3.2 1.3 0.2 0
3 4.6 3.1 1.5 0.2 0
4 5.0 3.6 1.4 0.2 0

数据概览

sns.FacetGrid(df, hue="target", size=5).map(plt.scatter, "sepal_length", "sepal_width").add_legend()
sns.FacetGrid(df, hue="target", size=5).map(plt.scatter, "petal_length", "petal_width").add_legend()
Out[4]:
<seaborn.axisgrid.FacetGrid at 0x2489c2947f0>

模型训练

# 拆分数据
from sklearn.cross_validation import train_test_split
x_train, x_test, y_train, y_test = train_test_split(df[['sepal_length','sepal_width']], df['target'], random_state=1)

# 训练
from sklearn.linear_model import LogisticRegression
model = LogisticRegression(C=1e5)    
model.fit(x_train,y_train)  

# 训练结果
print('Coefficient: n', model.coef_)
print('Intercept: n', model.intercept_)

# 检查得分
model.score(x_test,y_test)

Coefficient: n [[-37.8084961   34.25223621]
 [  0.23653235  -3.07735797]
 [  2.39247892  -0.42297463]]
Intercept: n [ 95.4960929    6.80619032 -13.62475114]
Out[8]:
0.7631578947368421

结果解释

绘制分割线和色块 + 散点(TODO)

分类结果的评价

对于分类结果，有以下4种情况：

相关(Relevant),正类 无关(NonRelevant),负类
被检索到(Retrieved) true positives(TP 正类判定为正类） false positives(FP 负类判定为正类,”存伪”)
未检索到(Not Retrieved) false negatives(FN 正类判定为负类,”去真”） true negatives(TN 负类判定为负类)

则可以用以下指标评价分类结果：

  • 精确率(accuracy)：
  • 准确率(precision): TP/(TP+FP)
  • 召回率(recall): TP/(TP+FN)
  • F1-Measure: 精确值和召回率的调和均值, 1/F1 = 1/P + 1/R

一般来说，准确率和召回率是互相影响的，理想情况下肯定是做到两者都高，但是一般情况下准确率高、召回率就低，召回率低、准确率高，当然如果两者都低，那是什么地方出问题了。

可以绘制R/P（precition/Recall）曲线来观察。

根据问题的不同，追求的指标也不同。比如，如果是做搜索，那就是保证召回的情况下提升准确率；如果做疾病监测、反垃圾，则是保准确率的条件下，提升召回。

更多的内容参考资料4[^4]。

参数说明

model = LogisticRegression(penalty=’l2’, dual=False, tol=0.0001, C=1.0,
fit_intercept=True, intercept_scaling=1, class_weight=None,
random_state=None, solver=’liblinear’, max_iter=100, multi_class=’ovr’,
verbose=0, warm_start=False, n_jobs=1)

  • penalty：惩罚项可以是l1或l2
    • l1: 向量中各元素绝对值的和，作用是产生少量的特征，而其他特征都是0，常用于特征选择
    • l2: 向量中各个元素平方之和再开根号，作用是选择较多的特征，使他们都趋近于0
  • dual: n_samples > n_features。默认False
  • tol
  • C: 目标函数约束条件：s.t.||w||1<C，默认值是0，C值越小，则正则化强度越大
  • fit_intercept: 是否需要常量
  • intercept_scaling:
  • class_weight:
  • random_state：随机数生成器
  • solver:
  • max_iter:
  • multi_class:
  • verbose:
  • warm_start:
  • n_jobs: 指定线程数

更进一步

还可以尝试更多的方法来改进这个模型，比如：

  • 加入交互项
  • 精简模型特性
  • 使用正则化方法
  • 使用非线性模型

参考资料

[^4]: 准确率(Accuracy), 精确率(Precision), 召回率(Recall)和F1-Measure