支持向量机(SVM)是一系列可用于分类、回归和异常值检测的有监督学习方法。本文讨论 SVM 在分类问题上的应用。
SVM 的优点包括:
* 在高维空间中行之有效。
* 当维数大于样本数时仍然可用。
* 在决策函数中只使用训练点的一个子集(称为支持向量),大大节省了内存开销。
* 用途广泛:决策函数中可以使用不同的核函数。提供了一种通用的核,但是也可以指定自定义的核劣势在于:
* 如果特征数量远大于样本数量,则表现会比较差。
* SVM不直接提供概率估计。这个值通过五折交叉验证计算,代价比较高SVM原理
处理分类问题,一个直接的思路是构建一条直线/超平面,将样本按照类别标签进行划分,然后用这条直线/超平面进行预测。
这条超平面最好能使得点到决策边界的距离最大化[^1]。
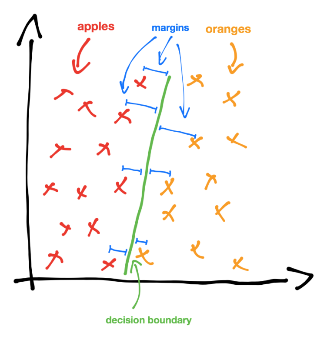
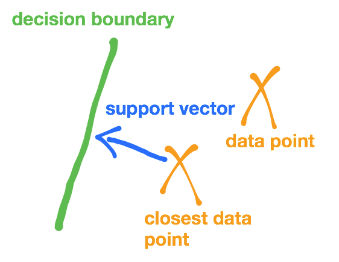
支持向量(support vectors),就是点到决策边界的最小间隔时的向量(由点出发垂直指向边界)。
如果样本线性不可分,就通过某种函数变换,使其变得线性可分,然后在求解直线/超平面。
这个函数变换,在SVM中称为核函数(kernel function)
最后,有可能会有个别的点无法正确分类,有时候要允许这种情况的发生。此时可以增加一个松弛变量/损失函数来适应这种情况。
在机器学习中,这种情况称之为正则,通常使用正则化参数来处理:
在我们的损失函数中添加一项:C(惩罚因子)。
对训练集的每一个数据点,给出特定的惩罚因子 c,c 越大表示偏离决策边界的损失越大。
更深入的理解,强烈推荐阅读资料[^2]。
scikit-learn对SVM的支持
Scikit-learn中的支持向量机同时支持密集样本向量( numpy.ndarray 和可通过 numpy.asarray 转化的数据类型)和
稀疏样本向量(任何 scipy.sparse 对象)。但是如果想用SVM对稀疏数据进行预测,则必须先在这些数据上拟合。
为了优化性能,应该使用C阶(C-Ordered) numpy.ndarray (密集的)或 scipy.sparse.csr_matrix (稀疏的),
并指定 dtype=float64 。
在分类问题上,可以使用 SVC , NuSVC 和 LinearSVC 这三个类。
SVC 和 NuSVC 两种方法类似,但是接受的参数有细微不同,而且底层的数学原理不一样。
LinearSVC 中,核函数被设定为线性的(线性核)。
用 scikit-learn的 SVM 分析鸢尾花数据集
import pandas as pd
import warnings
# 用来忽略seaborn绘图库产生的warnings
warnings.filterwarnings("ignore")
import seaborn as sns
import matplotlib.pyplot as plt
sns.set(style="white", color_codes=True)
%pylab inline
数据概览¶
from sklearn.datasets import load_iris
iris = load_iris()
df = pd.DataFrame(iris.data,columns=['sepal_length','sepal_width','petal_length','petal_width'])
df['target']=pd.Series(iris.target)
df.head()
sns.FacetGrid(df, hue="target", size=5).map(plt.scatter, "sepal_length", "sepal_width").add_legend()
sns.FacetGrid(df, hue="target", size=5).map(plt.scatter, "petal_length", "petal_width").add_legend()
模型训练¶
# 拆分数据
from sklearn.cross_validation import train_test_split
x_train, x_test, y_train, y_test = train_test_split(df[['sepal_length','sepal_width']], df['target'], random_state=1)
# 训练
from sklearn import svm
model = svm.SVC()
model.fit(x_train,y_train)
# 训练结果
# get support vectors
print(model.support_vectors_)
# get indices of support vectors
print(model.support_)
# get number of support vectors for each class
print(model.n_support_)
# 检查得分
model.score(x_test,y_test)
参考资料
[^1]: 感知机、逻辑回归、支持向量机- 伯克利机器学习入门教程
[^2]: 支持向量机通俗导论(理解SVM的三层境界)